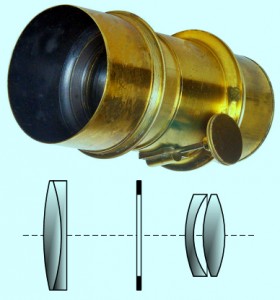
Figure 1 – An example of one of Joseph Petzval’s lenses.By Szőcs TamásTamasflex (Own work by uploader – Lens Photo by Андрей АМ) [CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0) or GFDL (http://www.gnu.org/copyleft/fdl.html)], via Wikimedia Commons
The bottom line is that early Daguerreotypists were plagued by the very high f-numbers of their cameras and the long exposures that they consequently demanded. The original lens that Daquerre used was a cemented doublet achromatic Chevalier 15-inch telescope objective with an f-number of 15.
Petzval’s innovation was to design a pair of doublets, where the second doublet compensated for the aberrations of the first. This produced a sharp image at the center with a softer focus off center as well a vignetting at the edges. Such a lens was ideal for portraiture, where the goal is to focus the eye on the subject not the background. Indeed, Petzval lenses are still manufactured today so as to achieve just this effect.
At f/3.6 this lens was almost 25 times faster than the original Chevalier lens. This made sitting times for portraits manageable, even for children. In this respect, Petzval may be credited with contributing significantly to the development of modern photography.
Petzval initially teamed with Voigtlander & Sons to produce his lens. Utimately, Petzval fell out with Peter Wilhelm Friedrich von Voigtländer (1812–1878) . Patent laws were problematic in the 19th century; so they continued to produce copies of his lens design and there was a dispute as to who held the legal right to manufacture these lens. In 1859, Petzval’s home was burglarized and his manuscripts and notes were destroyed. He never was able to reconstruct all of his previous work and he ultimately withdrew from society and died a destitute hermit in 1891. This seems, sadly, to be a common epilogue for the photographic geniuses of the 19th century.